In questo articolo cercheremo di comprendere alcune delle regole fondamentali per una guida sicura del carrello elevatore, cercando di spiegare quali sono i principi di fisica che ci accompagnano durante l’utilizzo del carrello elevatore.
Nell’immagine vengono rappresentate due persone che si trovano su una trave fissata ad un supporto con una cerniera, molti di noi da bambini avranno giocato in questo modo, ma alla base di questo gioco c’è un principio molto importante che si chiama Leva di primo genere, è molto importante conoscere questo principio quando si sollevano dei carichi, una errata applicazione comporterebbe una situazione svantaggiosa o nel caso della guida di un carrello elevatore, una situazione di pericolo, la caduta di un carico o addirittura il ribaltamento del carrello.
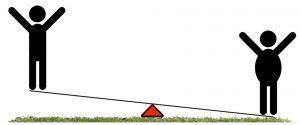
Per ora ci basta pensare che nel caso specifico, la persona più pesante molto probabilmente riuscirà a toccare il terreno mentre l’altra rimarrà sospesa in aria.
Ma cosa può fare la persona più leggera per arrivare a terra? Ci sono due possibilità, una è aumentare il proprio peso fino a superare quello dell’avversario, l’altra è spostarsi sulla punta della trave per aumentare la distanza dalla cerniera che in questa figura viene rappresentata dal triangolo rosso. Ma possiamo calcolare di quanto dovrà aumentare il proprio peso o di quanto dovrà arretrare? Certamente sì, la forza di rotazione che ognuno applica al fulcro è il prodotto tra il peso della persona e la distanza che ha dal fulcro, ad esempio se la persona a sinistra pesa 50 kg ed è posizionato a 2 metri, la forza di rotazione è di 50×2=100 (tralasciamo le unità di misura e concentriamoci sul concetto)
Alcuni esempi possono chiarire meglio le varie possibilità, ma prima introduciamo alcuni termini fondamentali. Il peso è dato dalla forza di gravità quindi lo possiamo chiamare semplicemente Forza, il punto nel quale avviene la rotazione ovvero la cerniera la chiameremo fulcro, la distanza del peso dal fulcro la chiameremo Braccio, mentre la forza di rotazione che viene prodotta la chiameremo Momento.

Due pesi uguali sono in equilibrio solo se anche la distanza dal fulcro è uguale.

Se uno dei due pesi è minore, per mantenere l’equilibrio, questo dovrà essere posizionato ad una distanza maggiore dal fulcro rispetto al peso più grande (aumento del braccio).

Se il peso più piccolo non ha sufficiente braccio, non riuscirà a bilanciare il peso più grande.

Se i due pesi sono uguali ma la distanza dal fulcro è diversa, il sistema non è in equilibrio, il peso con distanza maggiore dal fulcro crea un Momento maggiore (Forza di rotazione).
Ma cosa accade se al posto delle persone immaginiamo un carrello elevatore che trasporta un carico? Rappresentiamo con una freccia dritta la Forza, con una freccia circolare il Momento e al posto delle persone abbiamo da un lato il carrello elevatore e dall’altro il carico che stiamo trasportando. Posizionando la freccia che indica la forza rispettivamente sul baricentro del carico e sul baricentro del carrello, possiamo rappresentare il sistema in maniera semplificata e ragionare come abbiamo fatto con le figure precedenti.
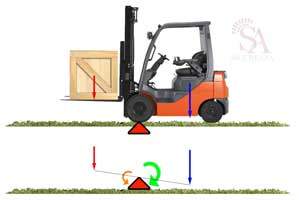
Nel caso sopra la situazione è la stessa che abbiamo visto nella prima figura dove sono rappresentate le persone, il peso del carico non è sufficiente a generare una forza di rotazione superiore a quella generata dal carrello, quindi può essere considerata “STABILE” e stiamo lavorando “in sicurezza”.
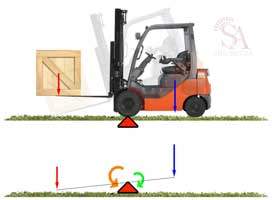
Se il carico viene posizionato verso la punta delle forche, potrebbe trovarsi ad una distanza eccessiva dal fulcro, il suo peso agisce su una leva più lunga e genera una forza di rotazione maggiore. In questo caso il carrello potrebbe ribaltarsi in avanti, ma per saperlo è necessario effettuare la moltiplicazione che abbiamo visto precedentemente: moltiplichiamo il peso del carico per la distanza del suo baricentro dal fulcro (ruota anteriore) poi moltiplichiamo il peso del carrello elevatore per la distanza del suo baricentro dal fulcro e confrontiamo i due risultati. Da questa considerazione possiamo dedurre che sicuramente il carico va posizionato il più vicino possibile ai montanti e quindi al fulcro in modo da avere il braccio più piccolo possibile!
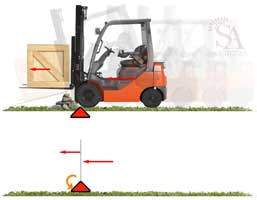
Se il carrello elevatore è in movimento, in gioco non c’è solamente la forza di gravità ma anche alcune forze orizzontali che permettono lo spostamento e la frenata del carrello stesso. Una delle forze che contribuiscono maggiormente alla instabilità del carrello elevatore è la forza di inerzia, quando freniamo bruscamente il nostro corpo tende ad andare in avanti come se qualcuno ci spingesse da dietro, la stessa “spinta” agisce anche sul carico che stiamo trasportando e sul carrello elevatore stesso. Durante la movimentazione del carico, potrebbe accadere di urtare un ostacolo o di effettuare una brusca frenata. In questo caso la forza di inerzia che agisce in orizzontale, contribuisce ad aumentare la rotazione che potrebbe generare il ribaltamento del carrello elevatore. Bisogna quindi mantenere il carico basso, frenare con cautela ed evitare buche ed ostacoli!
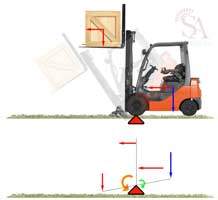
Se il carico viene trasportato ad un’altezza eccessiva, in caso di frenata o urto con un ostacolo, il ribaltamento è quasi certo! La forza di inerzia del carico agisce su una leva molto alta e genera un Momento elevato “forza di rotazione”. Più il carico è alto, maggiore è la probabilità di ribaltarsi!
Nell’immagine successiva si può notare che per la stabilità del carrello è essenziale che ilmomento stabilizzante Ms sia maggiore del momento ribaltante Mr, quindi (Ms>Mr).
Prima di andare avanti credo sia necessario spiegare la rappresentazione delle forze nella prossima immagine.
Le forze verticali dovute alla forza di gravità, quindi al peso del carico o del carrello elevatore, sono rappresentate con una freccia verticale bianca, mentre le forze orizzontali dovute all’inerzia sono rappresentate con delle frecce orizzontali bianche, sia le verticali che le orizzontali hanno come origine il baricentro (del carrello o del carico) rappresentato con un puntino giallo.
Nel nostro caso le due forze che agiscono nello stesso punto si sommano e possono essere rappresentate con una sola freccia obliqua, la risultante (ricavata con la regola del parallelogramma) colorata in blu denominata F1 e F2.
Il momento stabilizzante Ms si ottiene moltiplicando la risultante F1 (data dal peso del carrello elevatore più la forza di inerzia) per il braccio, (Ms=F1xb1). Il momento ribaltante Mr si ottiene moltiplicando la risultante F2 (data dal peso del carico più la forza di inerzia) per il braccio, (Mr=F2xb2). Quindi nel caso in cui il Mr sia maggiore di Ms si ha il ribaltamento frontale del carrello elevatore. Questa condizione di pericolo aumenta con l’aumentare della velocità e dell’altezza del carico dal suolo.
![]()
Da queste considerazioni fatte finora possiamo dedurre che, per mantenere la stabilità del carrello dobbiamo:
– ridurre la velocità di marcia e soprattutto non effettuare frenate improvvise, evitare ostacoli che possono far rallentare bruscamente il carrello
– trasportare i carichi rispettando il peso previsto dalle tabelle presenti sul libretto del carrello
– durante il trasporto mantenere sempre il carico basso
– cercare di mantenere il baricentro del carico vicino ai montanti inforcando completamente il carico